LeetCode 0100. Same Tree

Leetcode：Java

概要

題目：Same Tree

難度：Easy

本文

說明

題目會給我們兩個「二元樹」，分別為二元樹「p」和二元樹「q」。

而題目的要求是要我們判斷其兩者是否相同；而相同的定義是說，這兩顆「二元樹」有相同的結構以及相同的節點數值，如下：

解析一、遞迴法

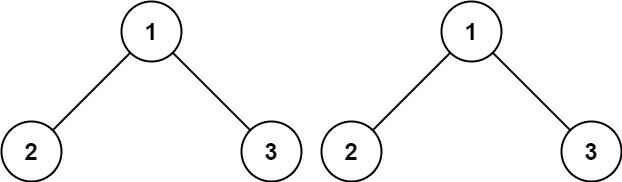
這題與之前解過的「Path Sum」是類似的，也是非常適合用「遞迴」來解。

這題算是偏基本的題型，概念就是，左邊比完，比右邊，完整代碼如下：

class Solution {
    public boolean isSameTree(TreeNode p, TreeNode q) {
        if (p == null && q == null) return true;
        else if (p == null) return false;
        else if (q == null) return false;
        else if (p.val != q.val) return false;
        return isSameTree(p.left, q.left) && isSameTree(p.right, q.right);
    }
}

稍微把程式碼寫得簡短一些，如下：

class Solution {
    public boolean isSameTree(TreeNode p, TreeNode q) {
        if (p == null) return q == null;
        if (q == null) return false;
        return isSameTree(p.left, q.left) && isSameTree(p.right, q.right) && (p.val == q.val);
    }
}

在「遞迴」的解題代碼中，我們是將「二元樹」拆成一個一個「樹節點」來分析，方法中的邏輯都是只針對自己當前的「樹節點」。

解析二、迴圈法

之前曾說過，在演算法中，若「遞迴」的解題方式，那通常都會有「迴圈」的解題方式。

上述我們說，「遞迴」的解法是將「二元樹」拆成一個一個來分析，事實上，「迴圈」也是如此，要有一點的變化。

什麼變化呢？

如果我們能將一顆「二元樹」的所有「樹節點」按照某演算規則將其變成「線性結構」，如下圖：

至於上述中的「某種規則」，其實就是在說「樹的遍歷」；所謂的「樹的遍歷」是說，指的是按照某種規則，不重複地存取某種樹的所有節點的過程。

一般來說，「樹的遍歷」可以分為「廣度優先搜尋」跟「深度優先搜尋」。

首先，「廣度優先搜尋」，英文是「Breadth-first Search」，簡稱「BFS」，其概念就是以橫向來遍歷樹，如下：

然後是，「深度優先搜索」，英文是「Depth-first Search」，簡稱「DFS」，其概念就是以縱向來遍歷樹；而「深度優先搜索」又會依照其遍歷方式不同，而分為「Pre-order」、「In-order」以及「Post-order」。

而由於篇幅所限，筆者在此只介紹，代碼中會用到的「Pre-order」，其流程與概念圖如下：

其實就是一次走到底，先遇到就先記錄，至於是「右先於左」還是「左先於右」，其實都可以的，上圖是「先左再右」，所以由「F」開始，依序是「B」、「A」，然後「A」的左，沒有，「A」的右，也沒，所以至此，第一條藍色的路線已經到頭，於是往回走，到「B」，由於剛剛是走左邊，所以這次走右邊，遇到「D」，然後就繼續往左走，遇到「C」，接著又到頭了，回走到「D」發現其右邊有「E」，到「E」，但「E」的左右都是盡頭，回頭，到「B」，因為左右都走過了，再回頭，到「F」，走其右邊，到「G」，因為沒左邊，往右走，到「I」，然後「H」，然後到頭了，回到「I」，右邊也是盡頭，回到「G」，再回到「F」，就遍歷完成。

所以其依序會是「F」、「B」、「Ａ」、「D」、「C」、「E」、「G」、「I」、「H」。

結著，當「二元樹」結構都變成「線性」結構後，倘若我們想要比較兩個二元樹是否一致，我們只需要將兩者的線性結構中的每一個節點「逐一比較」即可。

程式碼如下：

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public boolean isSameTree(TreeNode p, TreeNode q) {
        Stack<TreeNode> pTrees = preOrder(p), qTrees = preOrder(q);
        if (pTrees.size() != qTrees.size()) return false;
        Iterator<TreeNode> pIterator = pTrees.iterator(), qIterator = qTrees.iterator();
        while (pIterator.hasNext()) {
            TreeNode pNode = pIterator.next(), qNode = qIterator.next();
            if (pNode == null && qNode != null || qNode == null && pNode != null || pNode != null && pNode.val != qNode.val)
                return false;
        }
        return true;
    }

    public Stack<TreeNode> preOrder(TreeNode root) {
        Stack<TreeNode> rootTrees = new Stack<>(), orderTrees = new Stack<>();
        rootTrees.push(root);
        while (!rootTrees.isEmpty()) {
            TreeNode currNode = rootTrees.pop();
            orderTrees.push(currNode);
            if (currNode != null) {
                rootTrees.push(currNode.right);
                rootTrees.push(currNode.left);
            }
        }
        return orderTrees;
    }
}

別怕，雖然程式碼看起來非常長！

但其實就是兩部分，第一個部分，就是逐一比較「二元樹」線性結構中的每一個節點。

而關鍵在於「preOrder()」，該方法主要就是將「二元樹」遍歷，並建立該「二元樹」的「線狀結構」的方法；其實並不難理解，稍微放幾個「二元樹」，打印一下就知道邏輯了。

tags: leetcode java easy